概率论基础

June 3, 2018 4 分钟阅读

基本概念
集合运算
概率
条件概率
贝叶斯定理
- 举例一
- 举例二

基本概念

样本空间：随机试验E的所有可能结果组成的集合，记为S
样本点：样本空间的元素，即随机试验E的每个结果
随机事件：样本空间的子集，简称事件
不可能事件：每次试验都不会发生的事件，记为∅
必然事件：S是自身的子集，必然发生

集合运算

A⊂B：称事件B包含事件A
A∪B：A与B的和事件，$ \bigcup_{k=1}^{n}A_k $ 为 $ A_1、A_2、…A_n $的和事件
A∩B：A与B的积事件，$ \bigcap_{k=1}^{n}A_k $ 为 $ A_1、A_2、…A_n $的积事件
A-B：A与B的差事件，{$ x \mid x \in A 且 x \notin B $}
互斥：A∩B=∅，则称A与B互斥
对立：A∪B=S且A∩B=∅，则称A与B对立，或互称逆事件，A的对立事件也记为$ \bar{A} $
交换律：A∪B=B∪A，A∩B=B∩A
结合律：A∪(B∪C)=(A∪B)∪C，A∩(B∩C) = (A∩B)∩C
分配率：A∪(B∩C)=(A∪B)∩(A∪C)，A∩(B∪C)=(A∩B)∪(A∩C)
德摩根律：$ \overline{A∪B}=\overline{A}∩\overline{B}，\overline{A∩B}=\overline{A}∪\overline{B} $

概率

事件A的概率，记为P(A)
P(S)=1, P(∅)=0
可列可加性：$ A_1、A_2、…两两互斥，则P(A_1∪A_2∪…)=P(A_1)+P(A_2)+… $
逆事件：$ P(\overline A) = 1- P(A) $
加法公式：$ P(A∪B) = P(A) + P(B) - P(AB) $

条件概率

A事件发生情况下B事件的概率：

$ P(B\mid A) = \frac{P(AB)}{P(A)} $
乘法定理：

$ P(AB) = P(B \mid A)P(A) $
划分：

$ B_1、B_2、…、B_n两两互斥，且B_1∪B_2∪…∪B_n=S，则称B_1、B_2、…、B_n是样本空间S的一个划分 $
全概率公式：

$ P(A)=P(A \mid B_1)P(B_1)+P(A \mid B_2)P(B_2)+…+P(A \mid B_n)P(B_n) = \sum_{k=1}^nP(A \mid B_k)P(B_k) $
贝叶斯(Bayes)公式：

$ P(A \mid B)=P(A)\frac{P(B \mid A)}{P(B)}=P(A) \frac{P(B \mid A)}{ \sum_{k=1}^nP(B \mid A_k)P(A_k)}, (i为1、2…n中的一个) $

贝叶斯定理

$ P(A \mid B)=P(A)\frac{P(B \mid A)}{P(B)} $

P(A|B): 后验概率，B事件已经发生的情况下A事件的概率
P(A): 先验概率，A事件发生的概率
$ \frac{P(B \mid A)}{P(B)} $: 调整函数，A发生时B的概率除以 B的概率

意义：可以不断的通过有限信息，作出更进一步预测。

举例一

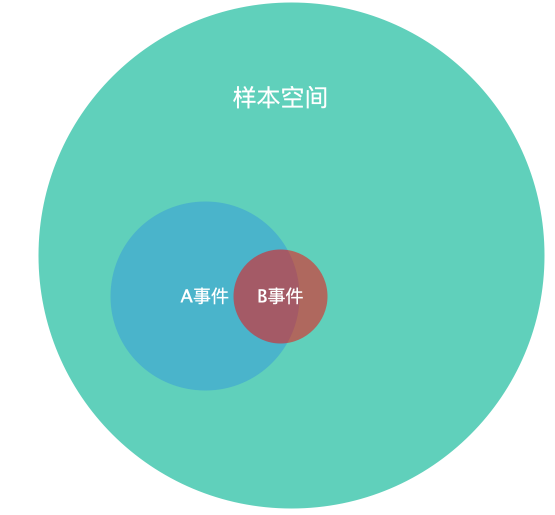
在样本空间内，A事件概率是30%，B事件概率是10%，A事件发生时B事件概率是15%。

那么B事件发生时A事件的概率P(A|B) = 30% * 15% / 10% = 45%

举例二

面试官面试，第一题适合的人90%答对，10%答错；不适合的人50%概率答对，50%概率答错。面试者初始印象50%，现在面试者答对了这道题目，那么那是合适人选的概率是多少？

解：

“面试者是合适人选”记作事件A，“答对题目”记作事件B，那么
P(A)= 50%，
P(B) = 50%*90% + 50%*50% = 70%，
P(B|A) = 90%
P(A|B) = P(A) * P(B|A) / P(B) = 64.3%
假如面试者答错了这道题目，答错题目记作b，那么合适人选的概率：
P(b)= 50%*10% + 50%*50 = 30%
P(b|A) = 10%
P(A|b) = 50% * 10% / 30% = 16%
也就是说这道题目可能是一道简单的题目，适合用于排除不合适的人，但不能确定是合适的人

HarmonyHu

基本概念

集合运算

概率

条件概率

贝叶斯定理

举例一

举例二