卷积运算
基本概念
基本卷积形式如下(NHWC格式):

输入为[1,32,32,3],filter为[10, 5, 5, 3],输出为[1, 28, 28, 10]
input
输入,一般维度表示为[n, ih, iw, ic]
filter
卷积核,一般维度表示为[oc, kh, kw, ic]
padding
填充。一般用于保持尺寸,比如图中想要使输出为32x32,则padding为[2,2,2,2],对输入边缘补0。
也有的卷积支持补常数。
strides
步进。filter在input上滑动时的步长,默认为1。一般做下采样时>1,比如h和w的strides为[2,2],则输出为[1, 14, 14, 10]。
dilations
膨化。默认是[1,1,1,1],对filter膨胀,如下图:
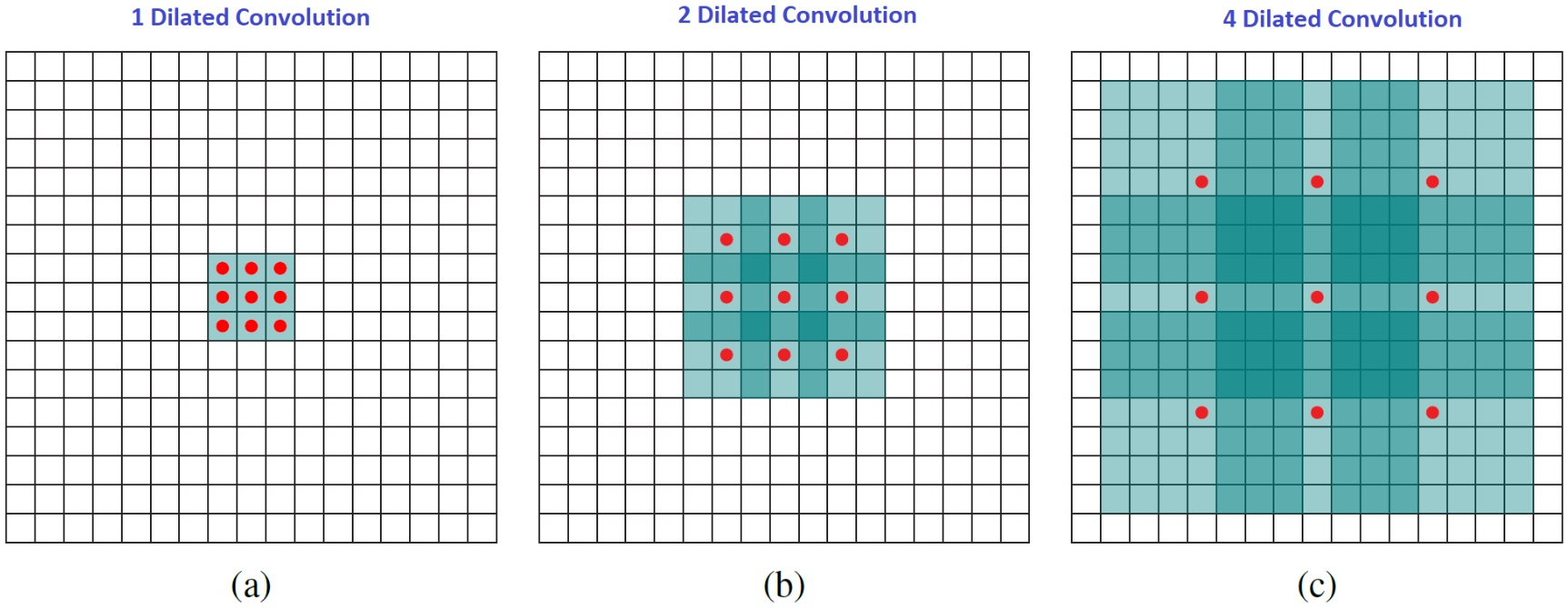
inserts
插入。对input按间隔插入0,高级的硬件应该可以插入常量。默认h和w的inserts为[0,0]。一般做上采样时>0,比如h和w的inserts为[1,1],则输出为59x59。
output
输出维度为[n, oh, ow, oc]
其中$ oh = ((ih-1) \times (h_{insert} + 1) + 1 + pad_{top} + pad_{bottom} - kh) \div h_{stride} + 1 $,ow同理
Group Conv
假如卷积核有N个,群数量为g。群卷积的操作为,将卷积核分为g份,每份N/g个。然后每份与输入做卷积,最后合并。如下对比图:
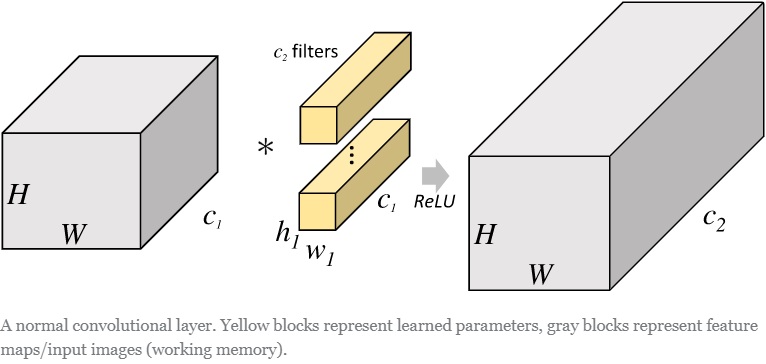
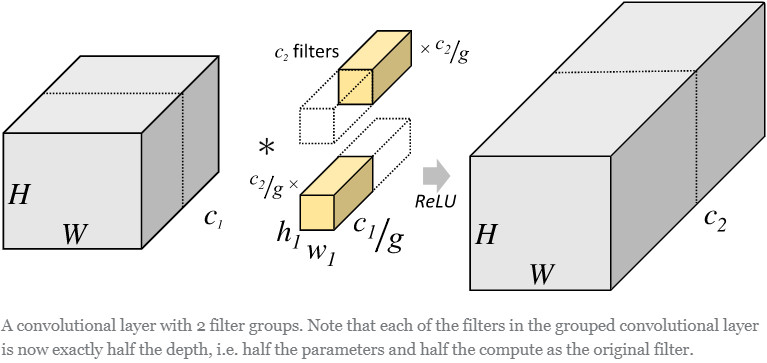
group conv通用用于减少参数量。
kernel可以表示为[g, oc/g, ic/g, kh, kw],参数量为 oc * ic * kh * kw / g
深度卷积时g = ic = oc,kernel对应为[ic, 1, 1, kh, kw],参数量为 oc * kh * kw
正常卷积核为[oc, ic, kh, kw],参数量为oc * ic * kh * kw
快速卷积(Winograd)
winograd算法最早是1980年Terry Winograd提出,Winograd快速卷积算法,出自CVPR 2016的paper:Fast Algorithms for Convolutional Neural Networks。此处学习来自:卷积神经网络中的Winograd快速卷积算法
一维卷积举例
输入是1维数据[d0, d1, d2, d3],卷积核是[g0, g1, g2],通常卷积计算如下:
\[F(2, 3) = \left[ \begin{array}{lll}{d_{0}} & {d_{1}} & {d_{2}} \\ {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right] \left[ \begin{array}{l}{g_{0}} \\ {g_{1}} \\ {g_{2}}\end{array}\right]=\left[ \begin{array}{c}{r_0} \\ {r_1}\end{array}\right]\] \[\begin{array}{l}{r_{0}=\left(d_{0} \cdot g_{0}\right)+\left(d_{1} \cdot g_{1}\right)+\left(d_{2} \cdot g_{2}\right)} \\ {r_{1}=\left(d_{1} \cdot g_{0}\right)+\left(d_{2} \cdot g_{1}\right)+\left(d_{3} \cdot g_{2}\right)}\end{array}\]需要6次乘法和4次加法。
采用Winograd算法,算法如下:
\[F(2,3)=\left[ \begin{array}{lll}{d_{0}} & {d_{1}} & {d_{2}} \\ {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right] \left[ \begin{array}{l}{g_{0}} \\ {g_{1}} \\ {g_{2}}\end{array}\right]=\left[ \begin{array}{c}{m_{1}+m_{2}+m_{3}} \\ {m_{2}-m_{3}-m_{4}}\end{array}\right]\] \[\begin{array}{ll}{m_{1}=\left(d_{0}-d_{2}\right) g_{0}} & {m_{2}=\left(d_{1}+d_{2}\right) \frac{g_{0}+g_{1}+g_{2}}{2}} \\ {m_{4}=\left(d_{1}-d_{3}\right) g_{2}} & {m_{3}=\left(d_{2}-d_{1}\right) \frac{g_{0}-g_{1}+g_{2}}{2}}\end{array}\]其中g本身的运算可以提前算好,一共运算次数为8个加减法和4个乘法。
Winograd展开后与原始卷积结果相同。但是通常乘法运算时间比较长,所以winograd算法是通过增加加减法减少乘法来实现加速。
二维卷积举例
输入是二维数据,维度为[4, 4],卷积核为[3, 3],进行Winograd转换如下:
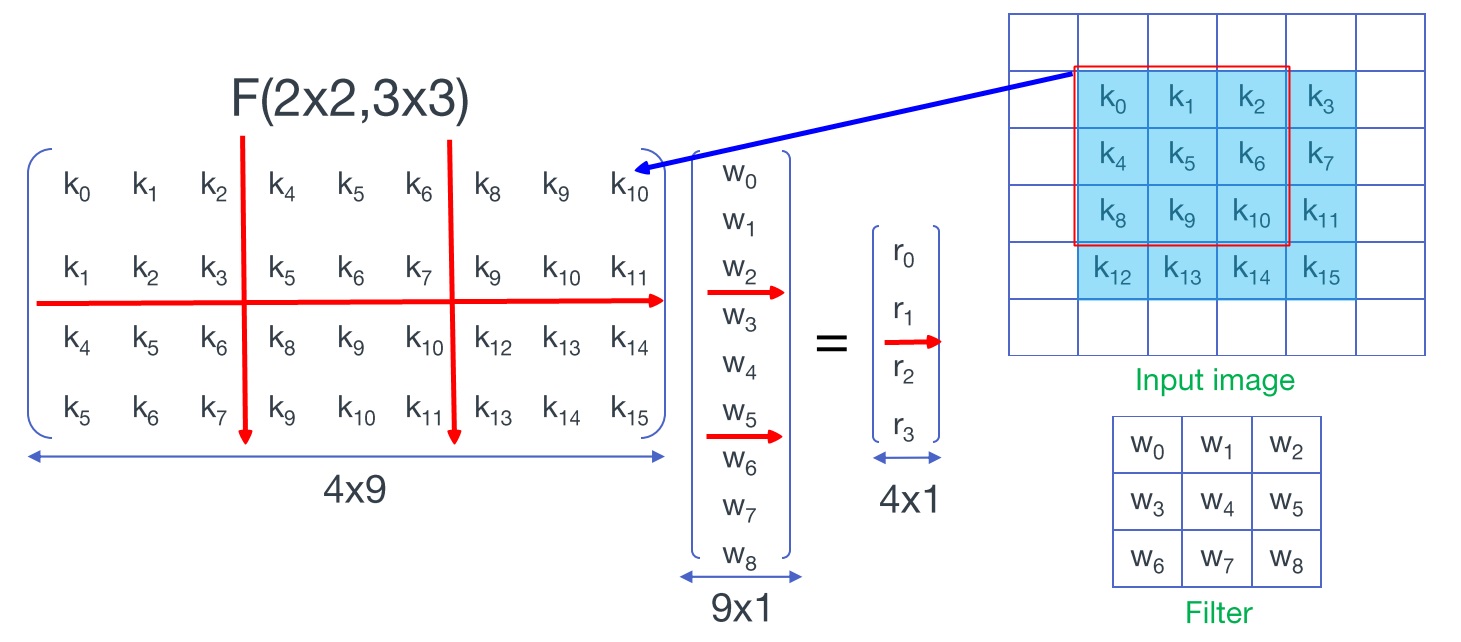
将卷积核的元素拉成一列,将输入信号每个滑动窗口中的元素拉成一行。注意图中红线划分成的分块矩阵,每个子矩阵中重复元素的位置与一维时相同,同时重复的子矩阵也和一维时相同,如下所示:
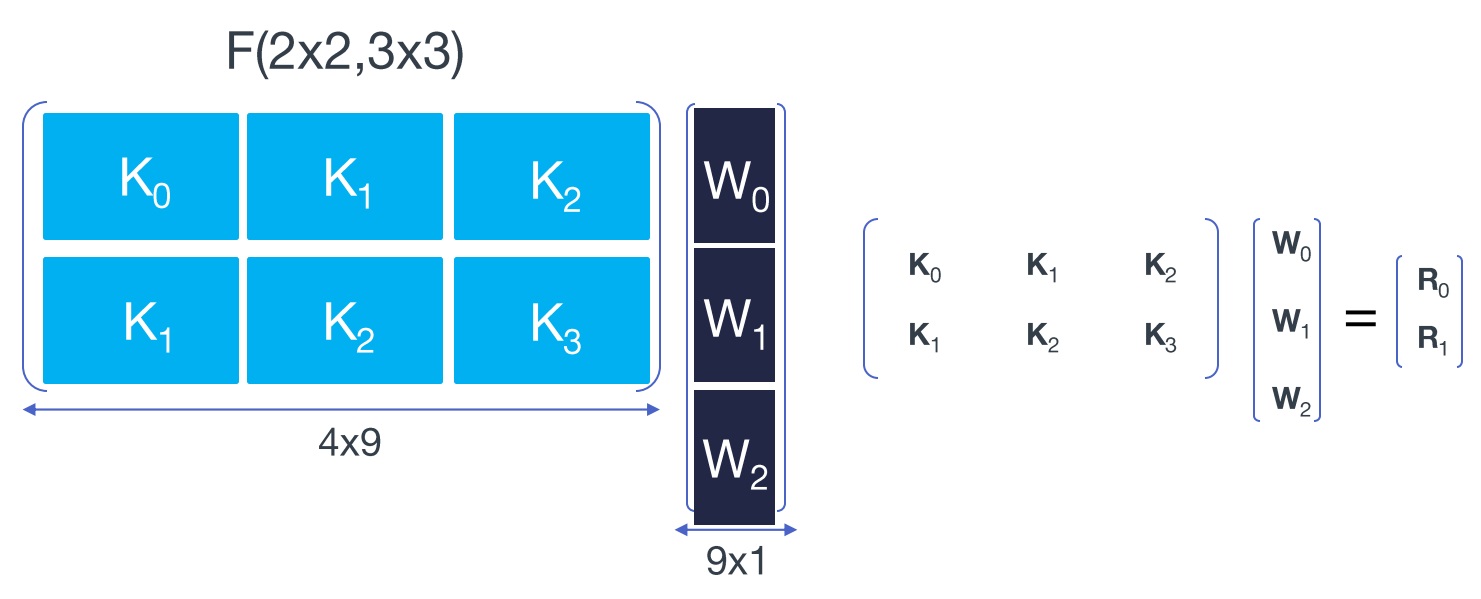
每个子矩阵再用Winograd算法转换,如下:

Deconvolution
Deconvolution是Convolution的逆操作。Convolution是将大尺寸feature map转换成小尺寸feature map,而Deconvolution是将小feature map转换成大feature map。两者shape计算过程对比:
# Convolution:
kernel = ic * oc * kh * kw
on = in
oh = (ih + 2 * pad_h - kh)/sh + 1
ow = (iw + 2 * pad_w - kw)/sw + 1
# Deconvolution:
kernel = ic * oc * kh * kw
on = in
oh = (ih - 1) * sh + kh - 2 * pad_h
ow = (iw - 1) * sw + kw - 2 * pad_w
计算过程
deconv计算过程与conv过程类似,简单来说就是先根据stride对输入补0,然后做卷积。
以input为3x3,kernel为3x3,stride =2举例:
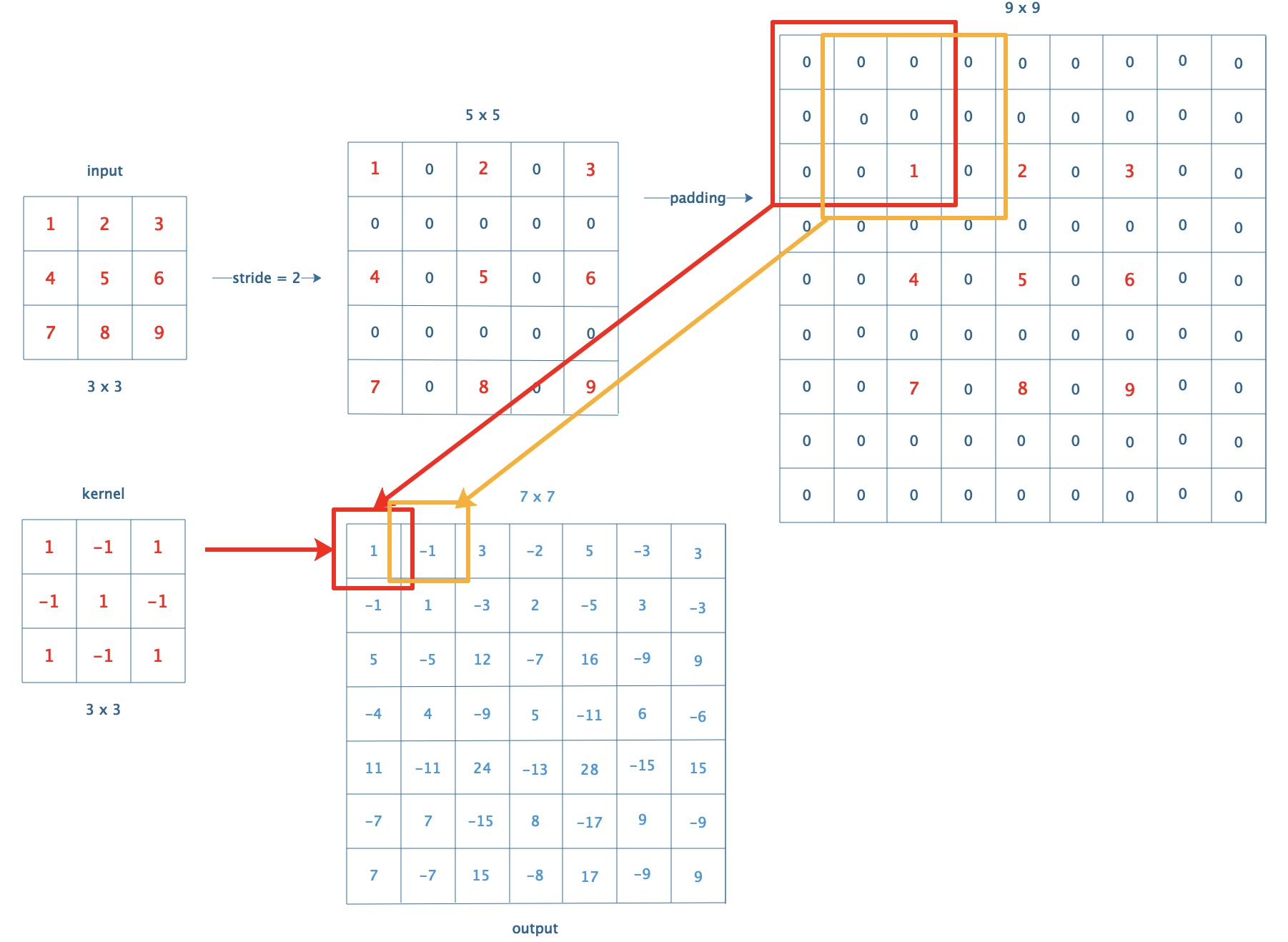
可以看出DeConv其实可以用Conv (inserts = [1,1])来实现
可变卷积
相关论文:CenterNet: Keypoint Triplets for Object Detection
相关代码:Deformable-ConvNets
与通常的卷积相比,kernel存在offset(偏移)和mask(权重)。
如图中所示,通过卷积计算结果2/3作为offset,1/3用sigmoid得到mask。模型结构类似如下:
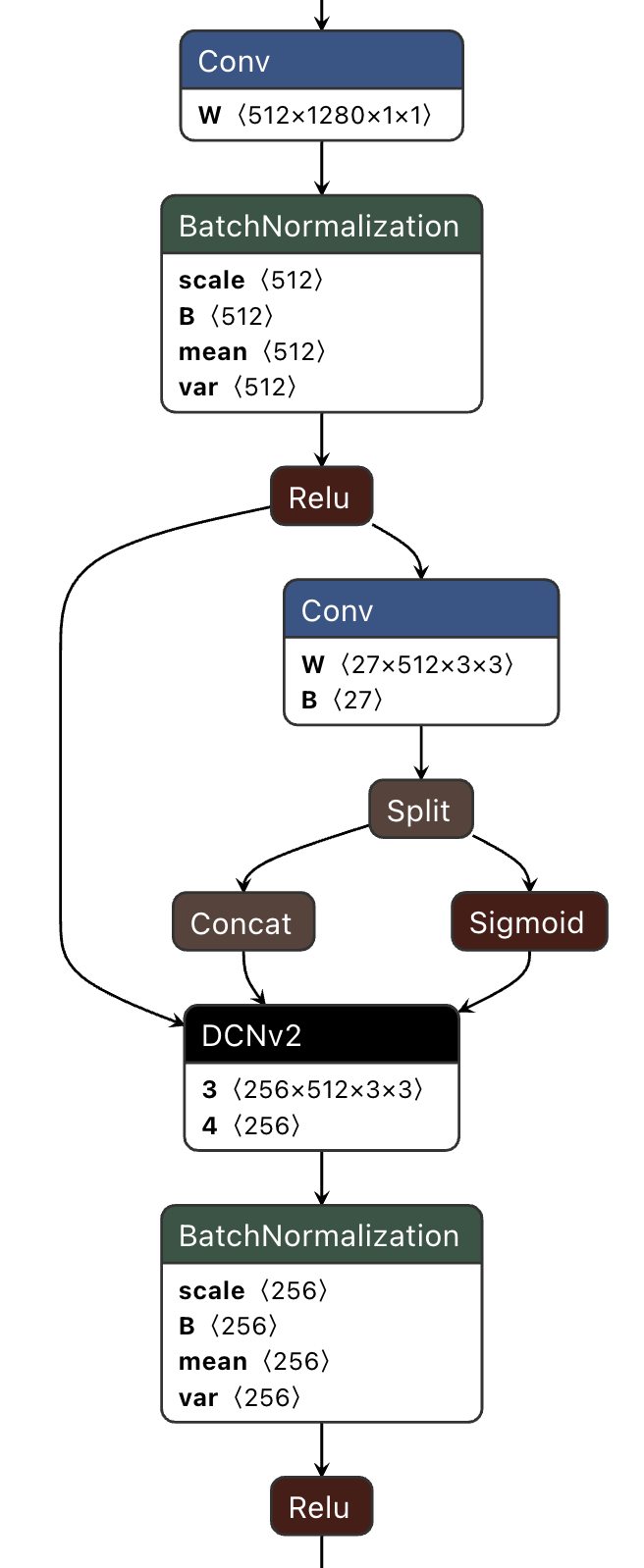
注:sigmoid是[0,1]的范围,通用用于表示权重,像lstm网络中的遗忘门。
运算过程大致如下:
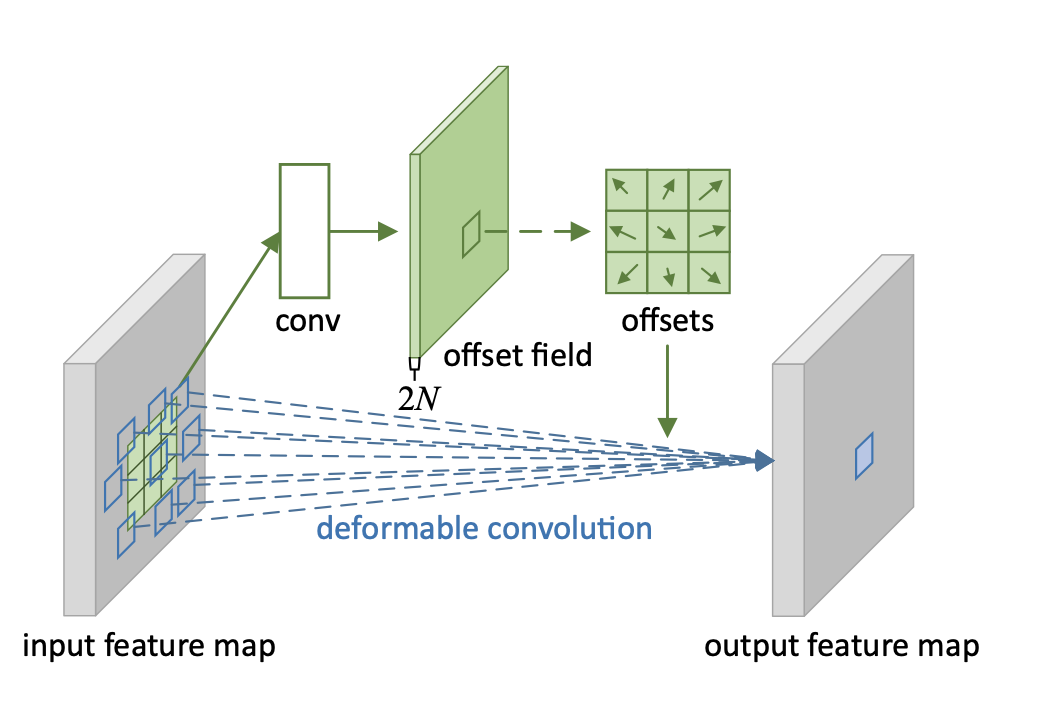
offset运算
offset表示kernel实际运算的位置的h和w的偏移,是浮点数。偏移后的位置,是4个点的中间某个位置,通过双线性插值计算该位置的取值。计算方法如下:
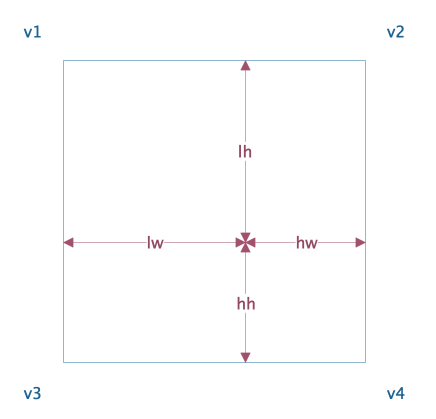
v = (v1 * hw * hh) + (v2 * lw * hh) + (v3 * hw * lh) + (v4 * lw * lh)
简单说就是根据该点与相邻4个点的距离的比重取值,距离越近占比越高。
运算完后再乘以权重,取最终值:
v = v * mask
