常见算子操作
激活函数
Relu
\[f(x) = \begin{cases} x,\quad & if & x \ge 0 \\ 0,\quad & if & x \lt 0 \end{cases}\]LeakyRelu
\[f(x) = \begin{cases} x,\quad & if & x \ge 0 \\ x \times negative\_slope,\quad & if &x \lt 0 \end{cases}\]PRelu
\[f(x) = \begin{cases} x,\quad & if & x \ge 0 \\ x \times slope\_data[c],\quad & if &x \lt 0 \end{cases}\]Sigmoid
\[f(x) = \frac{1}{1 + e^{-x}}\]将变量映射到(0,1),S型曲线,求导方便,求导过程:$ f’(x) = \frac{e^{-x}}{(1+e^{-x})^2} = f(x)\times (1 - f(x)) $
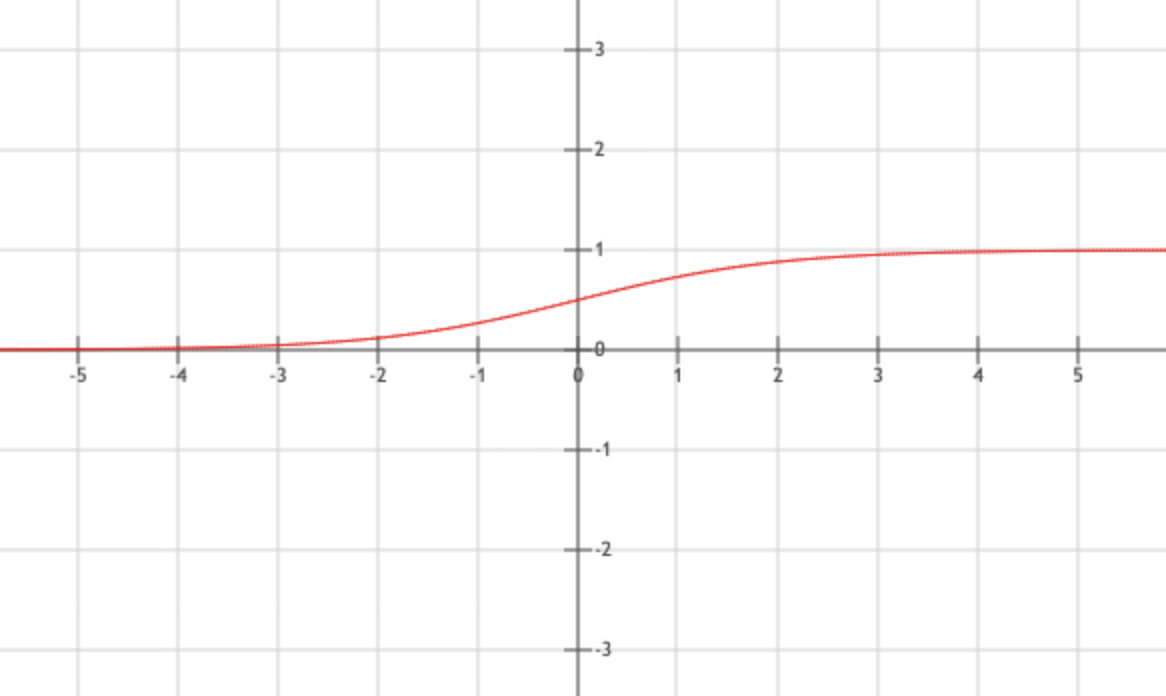
Tanh
\[f(x) = \frac{sinh(x)}{cosh(x)}=\frac{e^x - e^{-x}}{e^x + e^{-x}}\]将变量映射到(-1,1),S型曲线.
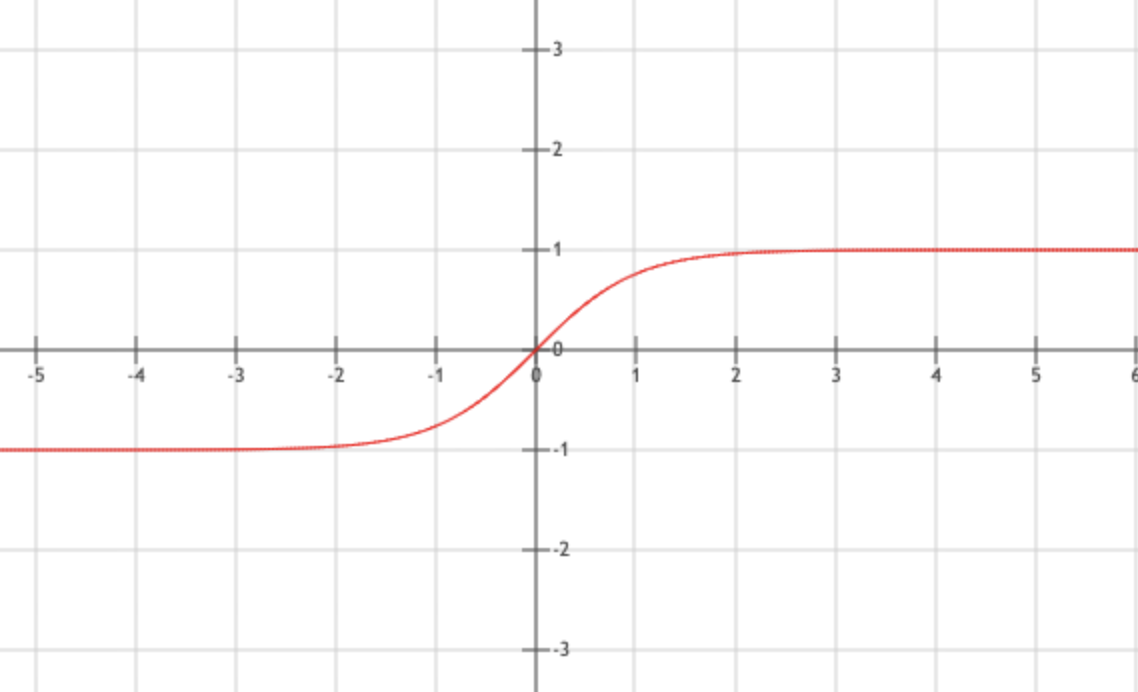
Mish
\[f(x) = x \times tanh(ς(x)),\quad 其中ς(x) = ln(1 + e ^x)\]YOLOv4网络使用的激活函数,类似relu,但是负值保持光滑非单调。
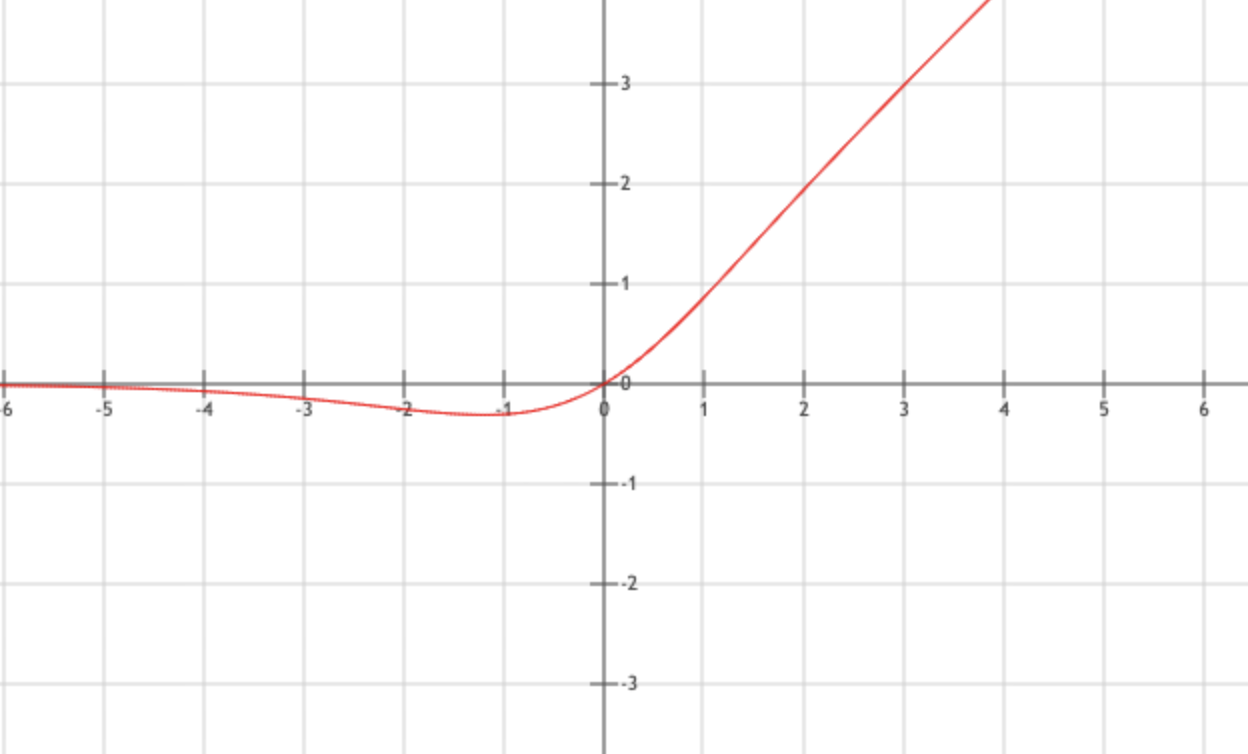
元素操作
Scale
\[f(x) = scale[c] \times x + bias[c]\]Power
\[f(x) = (scale \times x + shift)^{power}\]BatchNorm
\[mean = \frac{1}{m} \sum_{i=1}^{m}{x_i} \quad 求均值 \\ variance = \frac{1}{m} \sum_{i=1}^{m}{(x_i - mean)^2} \quad 求方差 \\ u_i = \frac{x_i - mean}{\sqrt{variance + eps}} \quad 归一化, eps用于防止除0 \\ y_i = \gamma \times u_i + \beta \Rightarrow BN_{\gamma,\beta}(x_i) \quad \gamma,\beta训练生成\]归一化,将网络层的输入转化到均值为 0方差为1的标准正态分布上,使梯度变化增大,加快训练收敛速度。
caffe中batchnorm,通常没有第四步,推理运算过程如下:
\[mean = blobs_0,\quad variance = blobs_1,\quad scale = blobs_2[0] \\ y_i = \frac{x_i - \frac{mean_c}{scale}}{\sqrt{\frac{variance_c}{scale} + eps}}\\\]LRN
\[b^i_{x,y} = a^i_{x,y} / \bigg(k + \alpha \sum^{min(N-1, i + n/2)}_{j = max(0, i- n/2)}(a^j_{x,y})^2\bigg)^\beta\]局部相应归一化,基本上只有googlenet在用。通俗来说就是局部相邻元素归一,分通道间相邻和通道内相邻。
LayerNorm
torch.nn.LayerNorm(normalized_shape: Union[int, List[int], torch.Size],
eps: float = 1e-05,
elementwise_affine: bool = True)
计算过程与BatchNorm相同,区别在于BatchNorm会在train阶段跟踪统计全局的均值方差;而LayerNorm不受train影响,推理时直接计算指定范围的均值方差。
向量操作
Pooling
\[\begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8 \end{bmatrix} \Rightarrow \begin{cases} \begin{bmatrix} 6 & 8 \end{bmatrix},\quad & if & max \\ \begin{bmatrix} 3.5 & 5.5 \end{bmatrix},\quad & if & average \end{cases}\]从大feature map转为小feature map,防止过拟合,减少参数
Upsample
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 & 1 & 2 & 2 \\ 1 & 1 & 2 & 2 \\ 3 & 3 & 4 & 4 \\ 3 & 3 & 4 & 4 \\ \end{bmatrix}\]上采样,用于扩大feature map,通常有这几种:
- 如图中所示,各个元素翻倍
- unpooling max,只有在pooling max位置填值,其余补0
- deconv,input填0后做卷积操作
Tile
\[\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 & 2 & 1 & 2 \\ 3 & 4 & 3 & 4 \\ 1 & 2 & 1 & 2 \\ 3 & 4 & 3 & 4 \\ \end{bmatrix}\]维度翻倍,上图是将(h,w)转换为(2h,2w)
Permute (Transpose)
\[\begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 & 5 \\ 2 & 6 \\ 3 & 7 \\ 4 & 8 \end{bmatrix}\]维度转换,比如图片三维HWC转换为CHW,可以用numpy如下操作:
x = np.transpose(x, (2,0,1))
Concat
\[\begin{bmatrix} 1 & 2 \end{bmatrix}, \begin{bmatrix} 3 & 4 \end{bmatrix}, \begin{bmatrix} 5 & 6 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{bmatrix}\]按指定维度进行合并。例子中axis=1;如果axis=0,则结果为[1 2 3 4 5 6]
Reshape
\[\begin{bmatrix} 1 & 2 & 3 & 4\\ 5 & 6 & 7 & 8 \end{bmatrix} \Rightarrow \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ 7 & 8 \end{bmatrix}\]不改变存储顺序,只改变tensor shape。
在caffe中由reshape_param.shape.dim指定新shape,如果dim=0,则保持不变;dim=-1,则指定为剩余维度。
Reorg
\[\begin{bmatrix} \begin{bmatrix} 1 & 3 & 2 & 4 \\ 5 & 7 & 6 & 8 \end{bmatrix} \end{bmatrix} \Rightarrow \begin{bmatrix} \begin{bmatrix} 1 & 2 \end{bmatrix}, \begin{bmatrix} 3 & 4 \end{bmatrix}, \begin{bmatrix} 5 & 6 \end{bmatrix}, \begin{bmatrix} 7 & 8 \end{bmatrix} \end{bmatrix}\]重组,stride指定间隔,reverse指定是否反向。令r = stride, 则:
当reverse为false时,$ [N,C,H,W] \Rightarrow [N, r^2 \times C, \frac{H}{r}, \frac{W}{r}] $
当reverse为true时,$ [N,C,H,W] \Rightarrow[N,\frac{C}{r^2}, H \times r, W \times r] $,注意$ C = r^2 \times \frac{C}{r^2} $
pixelshuffle
$ [N,C,H,W] \Rightarrow [N,\frac{C}{r^2}, H \times r, W \times r] $,注意 $ C = \frac{C}{r^2} \times r^2 $
与reorg reverse为true比较类似,区别在于C维降维的次序不同
Eltwise
\[\begin{bmatrix} \begin{bmatrix} 1 & 2 \end{bmatrix}, \begin{bmatrix} 3 & 4 \end{bmatrix}, \begin{bmatrix} 5 & 6 \end{bmatrix}, \begin{bmatrix} 7 & 8 \end{bmatrix} \end{bmatrix} \Rightarrow \begin{cases} \begin{bmatrix} 105 & 384 \end{bmatrix},\quad if \quad prod \\ \begin{bmatrix} 16 & 20 \end{bmatrix},\quad if \quad sum \\ \begin{bmatrix} 7 & 8 \end{bmatrix},\quad if \quad max \end{cases}\]Softmax
\[x_i = x_i - max(x_0,...,x_n) \\ y_i = \frac{e^{x_i}}{\sum^{n}_{j=0}e^{x_j}}\]通常用于分类网络中判断类别的概率。举例如下:
\[\begin{bmatrix} 3 & 1 & -3 \end{bmatrix} \Rightarrow \begin{bmatrix} 0 & -2 & -6 \end{bmatrix} \Rightarrow \begin{bmatrix} 0.88 & 0.12 & 0 \end{bmatrix}\]Argmax
\[\begin{bmatrix} 0 & 9 & 2 \\ 5 & 3 & 4 \end{bmatrix} \Rightarrow \begin{cases} [1 & 0 & 1], & if \quad axis = 0 \\ [1 & 0], & if & axis = 1 \end{cases}\]指定维度,得到最大值的index,对应操作numpy.argmax()。比如[n, c, h, w],如果axis = 0, 得到[c,h,w];如果axis = 1, 得到[n, h, w];如果 axis = 2, 得到[n, c, w]。
InnerProduct (FullyConnected)
二维矩阵运算,$ (M \quad N) \times (N \quad K) \Rightarrow (M \quad K) $
其他操作
GridSample
参见torch.nn.functional.grid_sample,输入和输出关系如下: \(Input_{(N, C, H_{in}, W_{in})}, Grid_{(N, H_{out}, W_{out}, 2)} \Rightarrow Output_{(N,C,H_{out},W_{out})}\) 网格在输入中采用,其中2对应Input的H和W坐标。坐标不一定是范围内的整数,
ScatterND
参见ScatterND,它等同于torch的索引操作,对局部向量进行更新。它对应三个输入,和一个输出。举例如下:
data = [1, 2, 3, 4, 5, 6, 7, 8]
indices = [[4], [3], [1], [7]]
updates = [9, 10, 11, 12]
output = [1, 11, 3, 10, 9, 6, 7, 12]
