统计距离
熵
Entropy, [ˈentrəpi], 熵,无序状态
信息量
信息不确定性越大,信息量越大。
假定X是随机事件集合,其中 $ p(x_0) $ 表示事件$ x_0 $的概率,那么事件$ x_0 $的信息量定义为 $ h(x_0) = - \log_2p(x_0) $。
信息熵
\[H(X) = -\sum^{n}_{i=1}{p(x_i)log_2p(x_i)}\]信息熵用来衡量事物的不确定性,信息熵越大,事物越具有不确定性。
相对熵 (KL散度)
设 p(x)、q(x) 是 离散随机变量 中取值的两个概率分布,则
对
的相对熵是:
另外有推导证明:$ DKL(p \parallel q) \ge 0 $
相对熵可以用来衡量两个概率分布之间的差异。该公式的意义在于,求p与q之间的对数差在p上的期望值。
交叉熵
设p(x)是真实分布,q(x)是非真实分布。使用q(x)来表示p(x)的编码长度,则:
\[H(p,q) = -\sum_{i=1}^{n}{p(x)log_2q(x)}\]另外有:
\[DKL(p \parallel q) = \sum_{i=1}^{n}{p(x_i)log_2\frac{p(x_i)}{q(x_i)}} = \sum_{i=1}^{n}{p(x_i)log_2{p(x_i)}} - \sum_{i=1}^{n}{p(x_i)log_2{q(x_i)}}\]可以得出:
\[DKL(p \parallel q) = H(p,q) - H(p)\]既可以理解为:用交叉熵比信息熵多出的部分,就是相对熵。
又有$ DKL(p \parallel q) \ge 0 $,得出 $ H(p,q) \ge H(p) $。
交叉熵广泛用于sigmoid和softmax函数中作为损失函数使用。
方差
方差
方差(variance): 用来度量随机变量和其数学期望(即均值)之间的偏离程度。
\[\sigma^2 = \frac{\sum{(x_i-\mu)^2}}{N} \\ \sigma^2为总体方差,x_i为样本变量,\mu为总体均值,N为样本数量\]标准差
标准差:方差的平方根,用来反映数据集的离散程度。
\[\sigma = \sqrt{\frac{\sum(x_i-\mu)^2}{N}}\]均方误差
均方误差:数据偏离真实值的距离平方和的平均数
均方根误差:均方误差的平方根
\[MSE = \frac{\sum(x-x_i)^2}{N} \\ 均方根误差 = \sqrt{MSE}\]欧式距离
以二维空间举例如图:
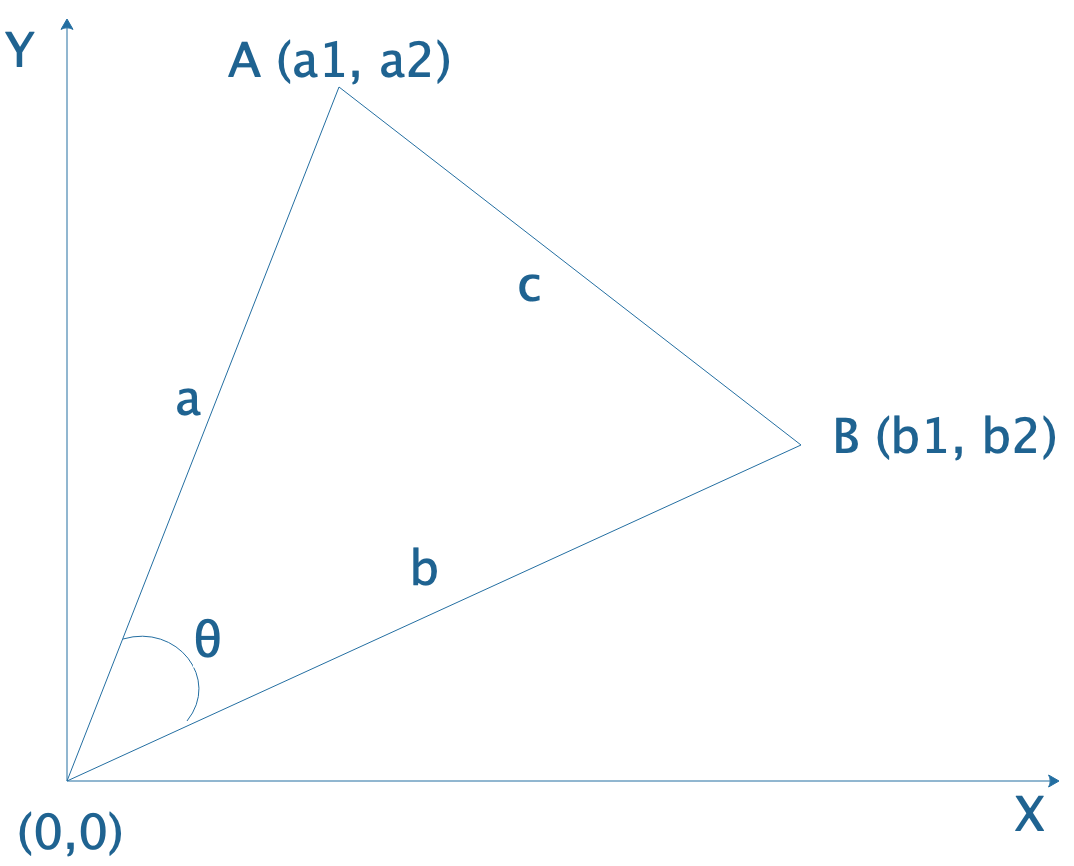
求A点与B点的欧氏距离。
在二维空间欧式距离就是两点的直线距离:
\[E(A,B) = c = \sqrt{(b_1-a_1)^2+(b_2-a_2)^2}\]多维空间同理:
\[E(p,q)= \sqrt{(p_1 - q_1)^2 + (p_2 - q_2)^2 + ... + (p_n - q_n)^2} = \sqrt{\sum_{i=1}^{n}(p_i - q_i)^2}\]欧式相似度:
\[euclidean\_similarity = \frac{1}{1 + E(p,q)}\]意义:用于对数值差异敏感的场景。
python实现
#!/usr/bin/env python
from math import *
def euclidean_distance(x,y):
return sqrt(sum(pow(a-b,2) for a, b in zip(x, y)))
print euclidean_distance([0,3,4,5],[7,6,3,-1]) #9.74679434481
余弦相似度
余弦定理:
\[c^2 = a^2 + b^2 - 2ab \:cos(\theta)\]进一步推导:
\[cos(\theta) = \frac{a^2+b^2 - c^2}{2ab} = \frac{a_1b_1 + a_2b_2}{\sqrt{a_1^2 + a_2^2} \times \sqrt{b_1^2+b_2^2}}\]多维空间同理:
\[cosine\_similary(A,B) = cos(\theta) = \frac{A\times B}{||A|| \times ||B||} = \frac{\sum_i^n{(A_i \times B_i)}}{\sqrt{\sum_i^n(A_i^2)} \times \sqrt{\sum_i^n{(B_i^2)}}}\]意义:值越趋于1越相似。一般用于数值不敏感,方向差异敏感的场景。
python实现
#!/usr/bin/env python
from math import *
def square_rooted(x):
return round(sqrt(sum([a*a for a in x])),3)
def cosine_similarity(x,y):
numerator = sum(a*b for a,b in zip(x,y))
denominator = square_rooted(x)*square_rooted(y)
return round(numerator/float(denominator),3)
print cosine_similarity([3, 45, 7, 2], [2, 54, 13, 15]) # 0.972
参考:
IMPLEMENTING THE FIVE MOST POPULAR SIMILARITY MEASURES IN PYTHON
SNR
信噪比:Signal-to-noise ratio,比值大于1时表明信号大于噪音,比值越大越好。
令标准数据为$A:[A_0, A_1, A2, …]$,采集数据为$ B:B_0,B_1,B2,…] $,则计算如下:
\[Noise = A - B = [A_0-B_0,A_1-B_1,...] \\ SNR = 10 \times log_{10}\frac{\sum(A_i-\bar{A)^2}}{\sum{(N_i-\bar{N})^2}}\]