Transformer
概述
论文地址[2017]:Attention Is All You Need
核心运算:$ Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}})V $
描述:查询(Query)到键值(Key-Value)的映射
模型结构
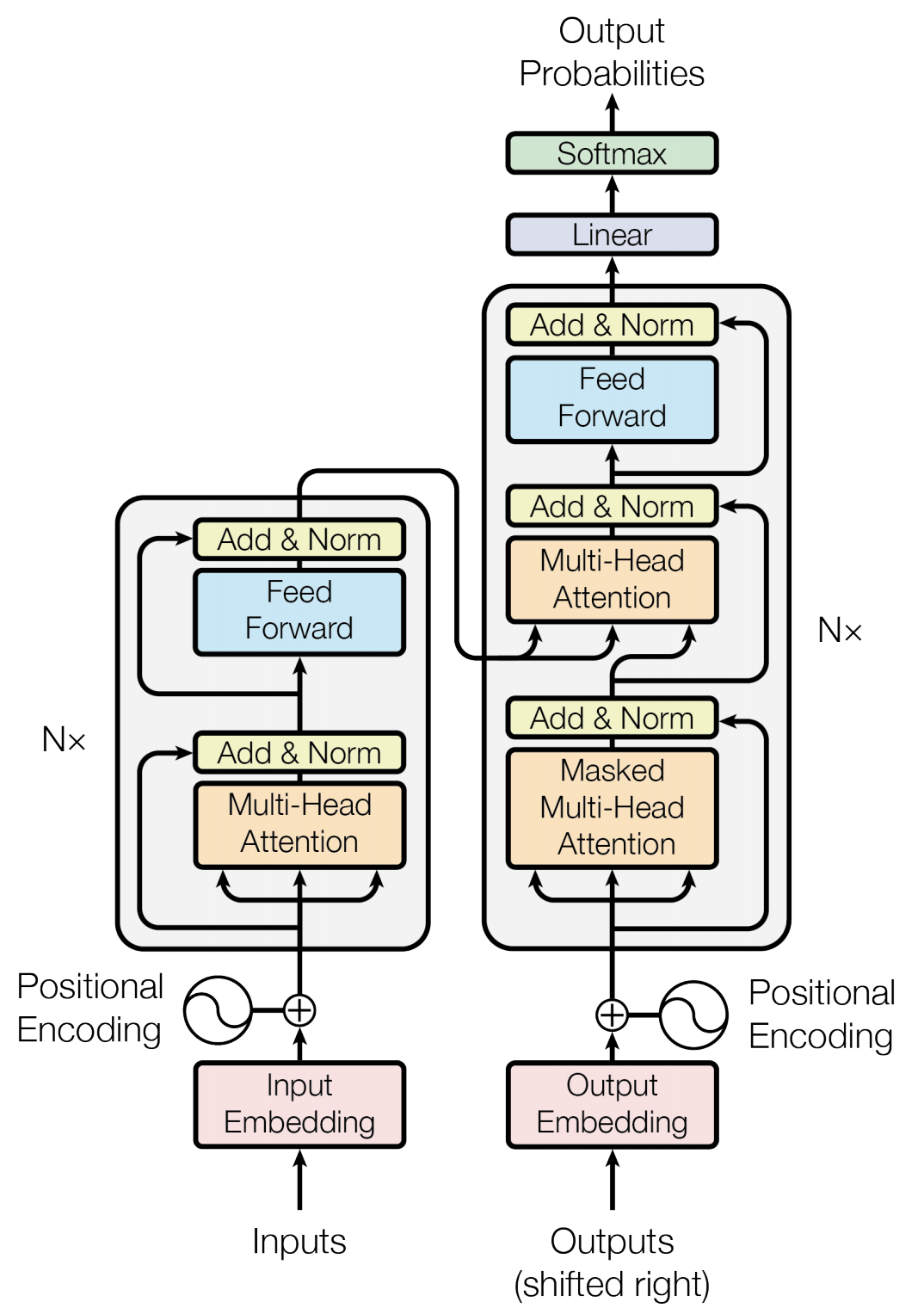
Embedding
\[X_{[batch\_size, seq\_len]} => X_{embedding[batch\_size,seq\_len, em\_dim]}\]向量嵌入,其中batch_size可理解为句子数量,seq_length可理解为单个句子的字数,embedding dimension为向量长度。
Embedding做的事情就是:将句子中的字转换成向量形式。
每个字对应的向量由Word2vec算法而定。
Word2vec
Word2vec由简单的神经网络模型生成,一般分两种:CBOW(Continuous Bag-of-Words)与Skip-Gram。
- CBOW输入是某个词的上下文词向量,输出是该词的词向量。适合小型数据量。如下图:
graph LR
W_t-2 --> hidden_layer
W_t-1 --> hidden_layer
W_t+1 --> hidden_layer
W_t+2 --> hidden_layer
hidden_layer --> W_t
- Skip-Gram输入是某个词的词向量,输出是上下文的词向量。适合大型数据量。如下图:
graph LR
W_t --> hidden_layer
hidden_layer --> W_t-2
hidden_layer --> W_t-1
hidden_layer --> W_t+1
hidden_layer --> W_t+2
Positional Encoding
\[PE_{(pos, 2i)} = sin(pos/10000^{2i/d_{model}}) \\ PE_{(pos, 2i+1)} = cos(pos/10000^{2i/d_{model}}) \\ X_{embedding}\ += PositionEncoding(X_{embedding})\]位置嵌入,由于self-attention运算后会使X的位置信息丢失,需要嵌入位置。
- pos:指字的位置,范围[0, max_sequence_length)
- i:指字的维度,范围[0, embedding dimension)
- dmodel:这里对应embedding dimension
Self-Attention
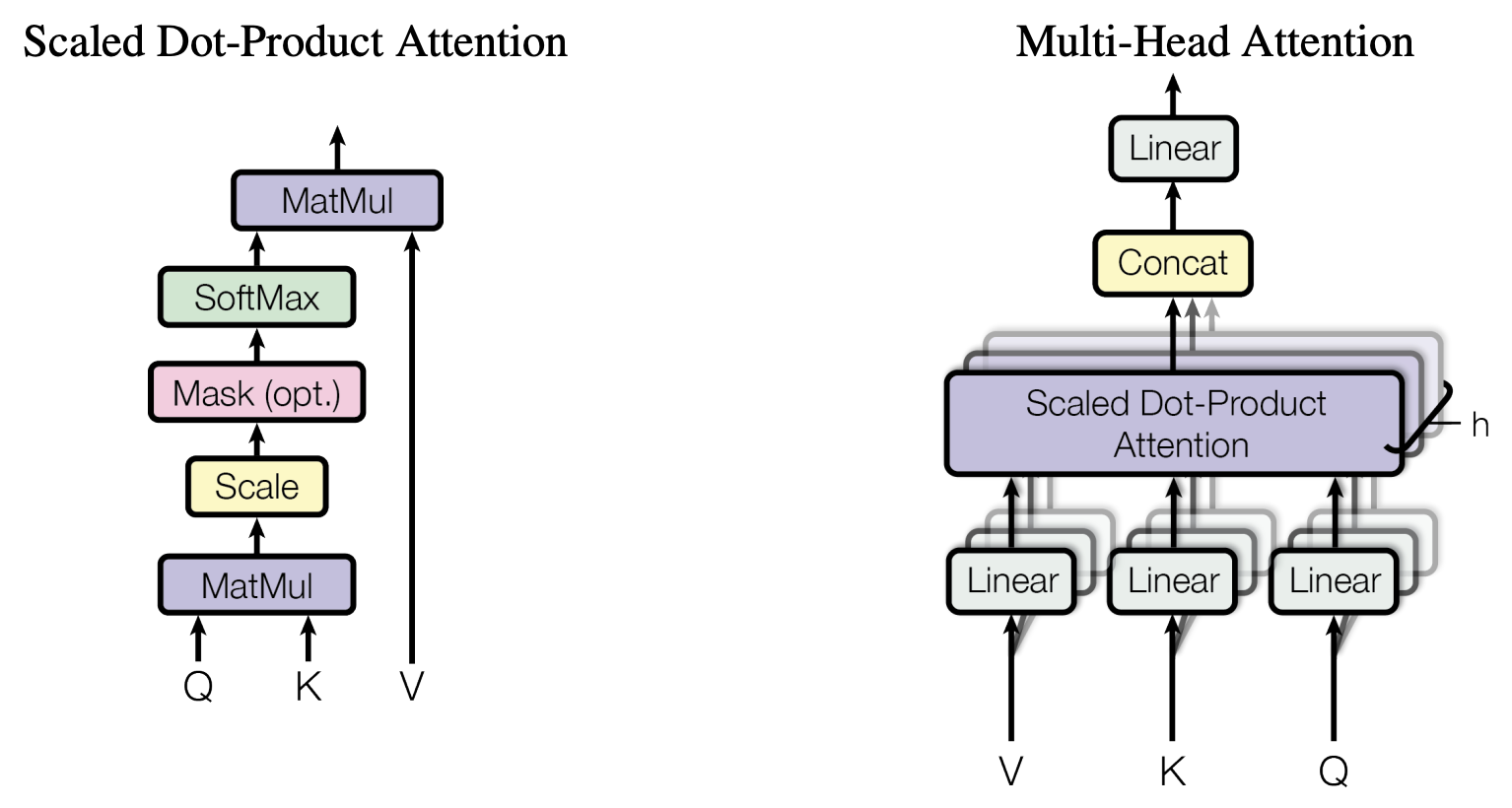
通常$ d_k = d_v = embedding_dim $,细节说明如下:
-
Q,K,V对应quary,key,value
-
√dk用于调节,使softmax输入为标准正态分布。Q和K的各个分量是标准归一化分布,也就是均值为0,方差为1。QKT 得到的结果,均值为0,方差为dk。
-
QKT 称注意力矩阵,维度为
[batch_size, h, seq_len, seq_len],Q与K对应向量越相似值越大,softmax后越大的值百分比越高 -
经过线性变换后Q,K,V的维度依然是
[batch_size, seq_len, em_dim],Attention之后的维度为[batch_size, seq_len, em_dim] -
由于语句有长有短,需要masking操作使超出部分无效。
multi head attention
\[head_i = Attention(QW_i^Q, KW_i^K, VW_i^V) \\ MultiHead(Q,K,V) = Linear(Concat(head1, ..., head_h)W^O)\]将embedding dim平均拆分成多份:head size = embedding dim / num of heads。
这样Q,K,W的维度为[batch_size, h, seq_len, em_dim/h]。
然后与V点积后维度为[batch_size, h , seq_len, em_dim/h]。
残差与归一化
\[X_{res} = X_{em}+ Attention(Q,K,V) \\ X_{attention} = LayerNorm(X_{res}) = \alpha \odot \frac{X_{ij}-\mu_i}{\sqrt{\sigma_i^2 + \epsilon}} + \beta\]防止梯度消失,加快收敛
前馈网络
\[FFN(x) = max(0, xW_1 + b_1)W_2 + b_2 \\ Res\ and\ LayerNorm\]线性映射和激活函数Pooling,然后再残差与归一化
循环重复
从Self-Attention到前馈网络循环操作
