Resize

• 概述
• 坐标转换模式
  • Half Pixel
  • Align Corners
  • Asymmetric
• 插值模式
  • Linear
  • Nearest
  • Cubic

概述

ONNX操作描述：Resize

参考代码：resize.py

坐标转换模式： half_pixel、align_corners、asymmetric、pytorch_half_pixel、tf_crop_and_resize

插值模式： linear、nearest、cubic

本文以 $ A[h_a, w_a] $ resize to $ B[h_b, w_b] $举例。

坐标转换模式

Half Pixel

将A中各元素摆放在$ h_a \times w_a $的区域中，将B中各元素摆放在$ h_b \times w_b $的区域中。

那么A中各点的坐标位置对应如下：

$ A_{[0,0]} => [0.5, 0.5]$

$ A_{[0,1]} => [0.5, 1.5]$

$ A_{[y,x]} => [0.5 + y, 0.5 + x] $

B中各元素位置同理。

如果是A resize to B，则先将B区域拉伸至A区域范围；如果是B resize to A，则先将A区域拉伸至B区域范围。

如下图所示：

[注：A拉伸至B，或者B拉伸至A都可以，不影响结果]

以图中A resize to B举例，则有：

$ scale_w = \frac{w_a}{w_b} $​

$ scale_h = \frac{h_a}{h_b} $​

那么经过变化后B中各点的坐标位置对应如下：

$ B_{[0,0]} => [0.5 \times scale_h, 0.5 \times scale_w] $​

$ B_{[0,1]} => [0.5 \times scale_h, 1.5 \times scale_w] $​

$ B_{[y,x]} => [(0.5+y) \times scale_h, (0.5+x) \times scale_w] $​

Align Corners

将A中各元素摆放在$ (h_a - 1) \times (w_a - 1) $的区域中，将B中各元素摆放在$ (h_b - 1) \times (w_b - 1) $的区域中。

那么A中各点的坐标位置，$ A_{[y,x]} => [y, x] $；B中各元素位置同理。

经拉伸后如下图：

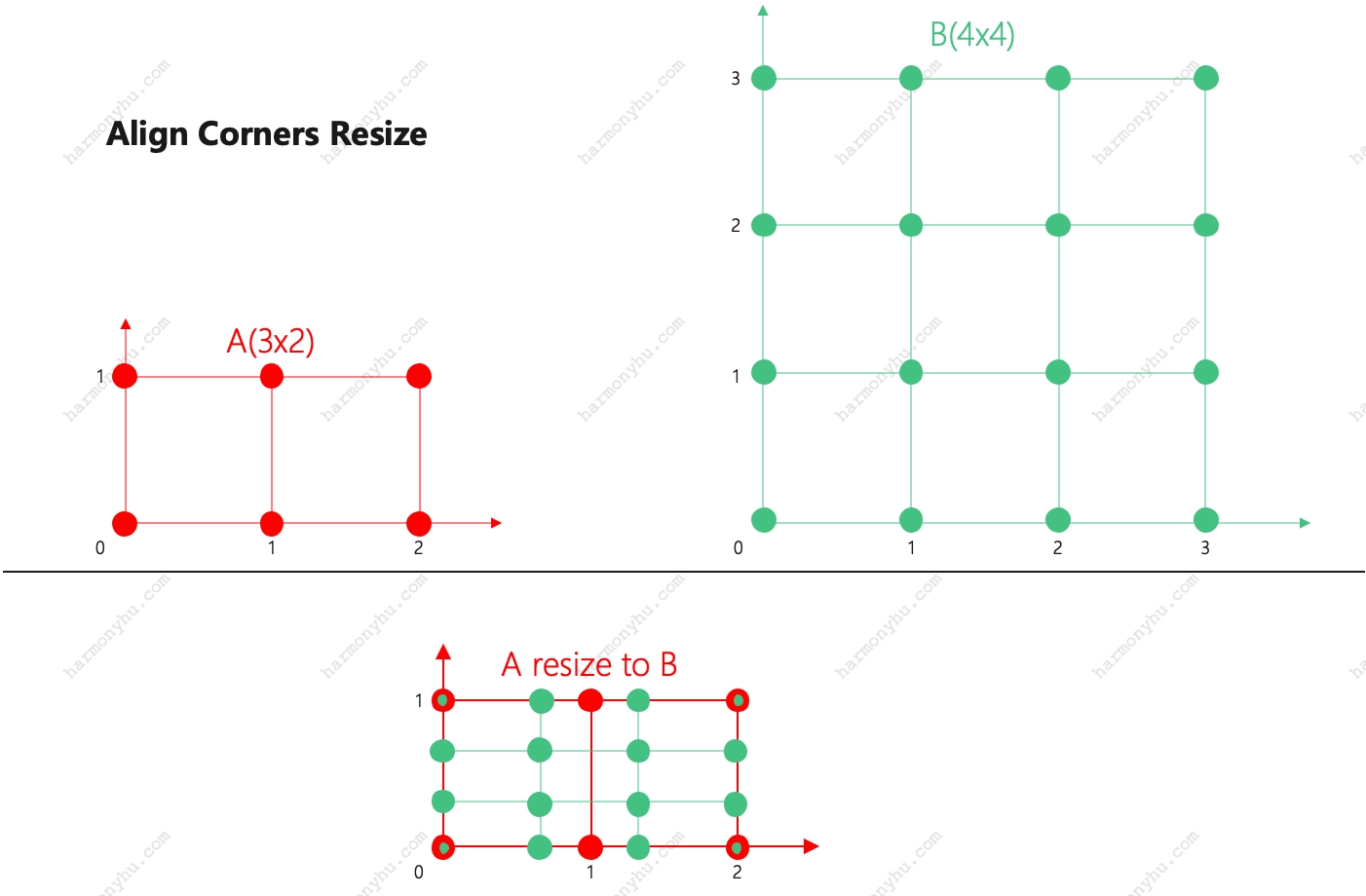
其中：

$ scale_w = \frac{w_a - 1}{w_b - 1} $​

$ scale_h = \frac{h_a - 1}{h_b - 1} $​

经过变化后B中各点的坐标位置对应如下：

$ B_{[0,0]} => [0 \times scale_h, 0 \times scale_w] $​

$ B_{[0,1]} => [0 \times scale_h, 1 \times scale_w] $​

$ B_{[y,x]} => [y \times scale_h, x \times scale_w] $​

Asymmetric

[ˌeɪsɪˈmetrɪk], 不对称的。

将A中各元素摆放在$ h_a \times w_a $​​的区域中，将B中各元素摆放在$ h_b \times h_b $​​的区域中。

那么A中各点的坐标位置，$ A_{[y,x]} => [y, x] $​；B中各元素位置同理。

经拉伸后如下图：

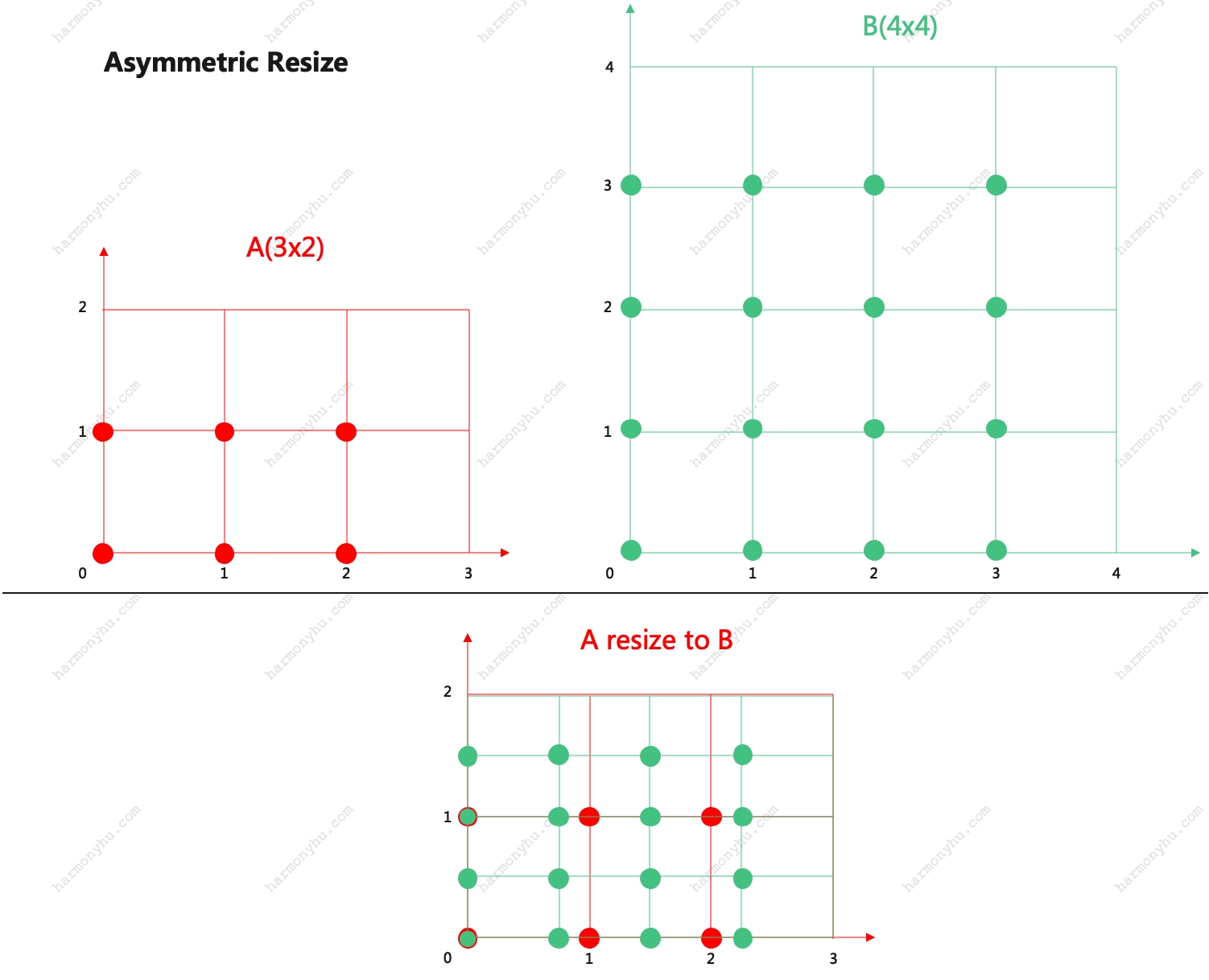
其中：

$ scale_w = \frac{w_a}{w_b} $​

$ scale_h = \frac{h_a}{h_b} $​​

经过变化后B中各点的坐标位置对应如下：

$ B_{[0,0]} => [0 \times scale_h, 0 \times scale_w] $​

$ B_{[0,1]} => [0 \times scale_h, 1 \times scale_w] $​

$ B_{[y,x]} => [y \times scale_h, x \times scale_w] $​

插值模式

Linear

取B点最近的四个A点，做加权平均值（双线性差值），得到B点的值。如果B点在w或h方向上超出A边缘，则在该方向上取A边缘值。计算方法如下（越靠近某个点，则该点权重越大，越接近该值）：

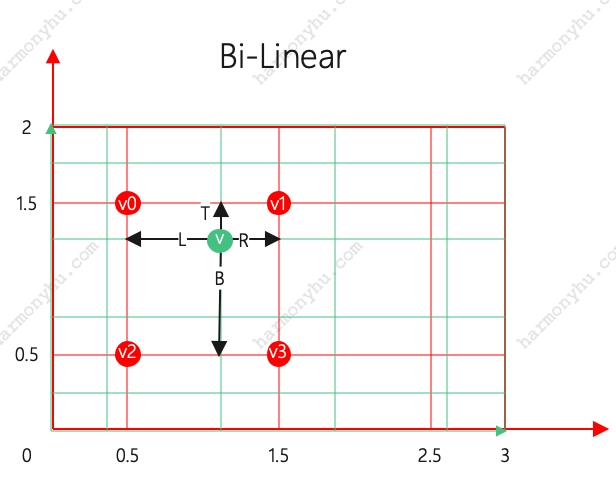
$ v = v0 \times (R \times B) + v1 \times (L \times B) + v2 \times (T \times R) + v3 \times (R \times B) $

Nearest

取B点最近的一个A点的值

Cubic

取B点最近的八个A点的值，做加权平均值